0%

Tower of Hanoi

Posted on In Disqus:

“汉诺塔”算法

Game towerofhanoi

题目：汉诺塔：三根杆子a、b、c，a杆由下到上按照从大到小的顺序穿了n个碟子，要求将n个碟子从a杆全部移动到c杆，移动结束后，碟子仍然按照由下到上从大到小的顺序排列，每次只能移动一个碟子，且小碟子不能放在大碟子下面。程序的每一行输出应该为：

moving disk x from pole i to pole j

其中，x是碟子的编号，从1开始一直到n，编号小的碟子是小碟子，i、j是杆的编号，为a、b或c

看了一些帖子，发现有一帖子说明特别简单易懂。于是引用了他博文的图片进行学习。

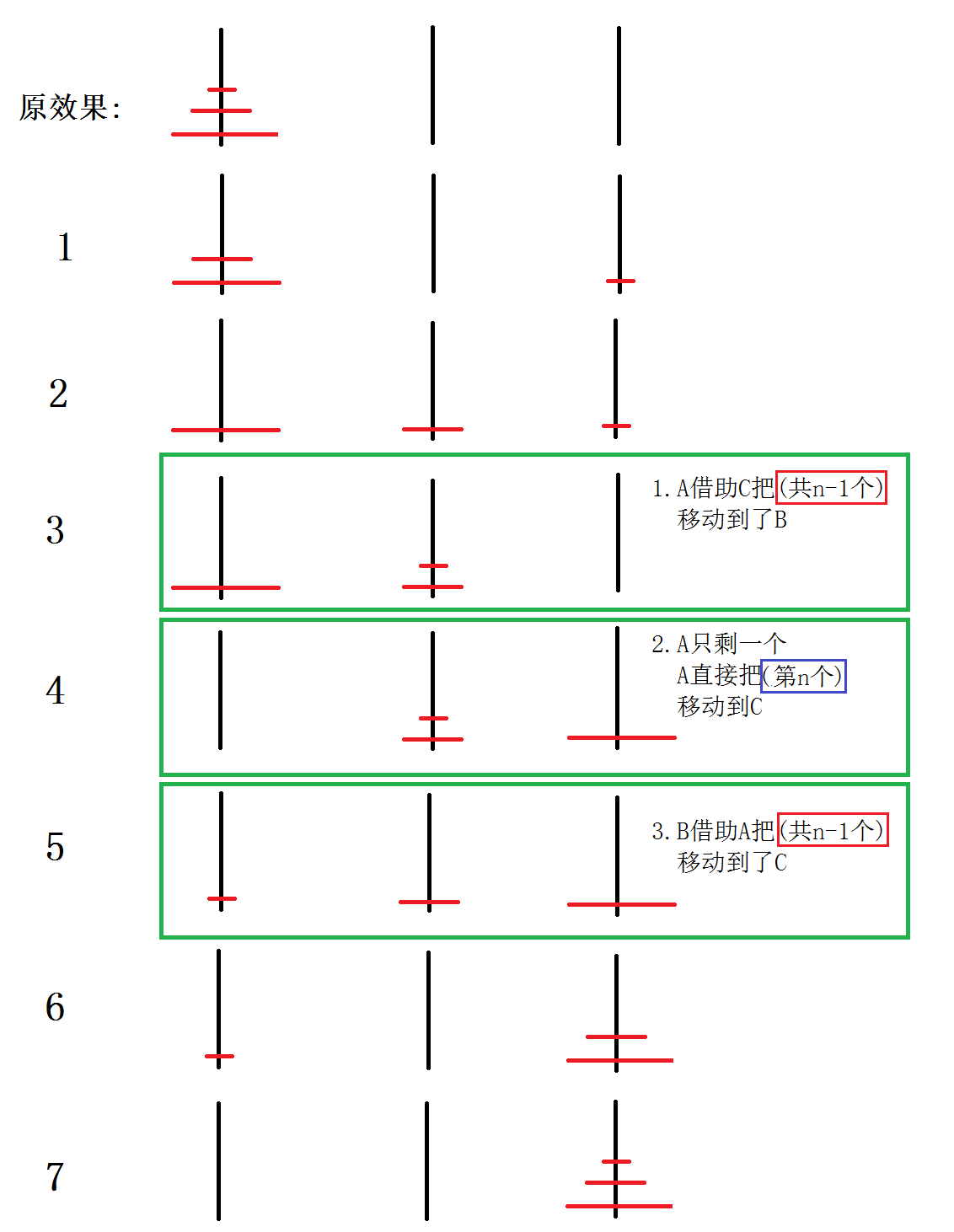
图中看出，只要抽象出主要的三步就能化繁为简。这刚好印证了递归的精华所在，如果不使用递归，是很难实现的。很多人说递归很难，其实递归是帮助我们简化问题。

  • A柱子把”共n-1”个盘借助C盘移动到B盘,完成一个大过程
  • A柱子把剩下的”第n”个盘直接移动到C盘,完成一个大过程
  • B柱子上的”共n-1”个盘借助A移动到C盘,又完成一个大过程

重复上面的大过程直至只剩下一个盘，于是就到了递归的结束条件。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
package main

import (
	"fmt"
	"strconv"
)

func hanoi(i int, steps *int, debug bool) {
	move(i, "A", "B", "C", steps, debug)
}

// a b c分别是柱子，i代表disk
func move(i int, a string, b string, c string, steps *int, debug bool) {
	*steps++
	// 每个n-1的整体的最底下的disk的移动，从a移动到c
	if i == 1 {
		if debug {fmt.Println("moving disk" + strconv.Itoa(i) + " from pole " + a + " to pole " + c)}
		return
	}
	// 将共i-1个disks从a按移动到b
	move(i - 1, a, c, b, steps, debug)
	if debug {fmt.Println("moving disk" + strconv.Itoa(i) + " from pole " + a + " to pole " + c)}
	// 将共i-1个disks从b按移动到c
	move(i - 1, b, a, c, steps, debug)
}

func activity(numOfDisks int, debug bool){
	steps := 0
	hanoi(numOfDisks, &steps, debug)
	fmt.Println(steps)
}

func main(){
	// n个碟子，3个木桩，求最小移动次数，结果是等于2的n次方减1
	debug := true
	activity(1, debug)
	fmt.Println()
	activity(2, debug)
	fmt.Println()
	activity(3, debug)
	fmt.Println()
	activity(4, debug)
	fmt.Println()
	activity(5, debug)
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
Result

moving disk1 from pole A to pole C
1


moving disk1 from pole A to pole B
moving disk2 from pole A to pole C
moving disk1 from pole B to pole C
3


moving disk1 from pole A to pole C
moving disk2 from pole A to pole B
moving disk1 from pole C to pole B
moving disk3 from pole A to pole C
moving disk1 from pole B to pole A
moving disk2 from pole B to pole C
moving disk1 from pole A to pole C
7


moving disk1 from pole A to pole B
moving disk2 from pole A to pole C
moving disk1 from pole B to pole C
moving disk3 from pole A to pole B
moving disk1 from pole C to pole A
moving disk2 from pole C to pole B
moving disk1 from pole A to pole B
moving disk4 from pole A to pole C
moving disk1 from pole B to pole C
moving disk2 from pole B to pole A
moving disk1 from pole C to pole A
moving disk3 from pole B to pole C
moving disk1 from pole A to pole B
moving disk2 from pole A to pole C
moving disk1 from pole B to pole C
15


moving disk1 from pole A to pole C
moving disk2 from pole A to pole B
moving disk1 from pole C to pole B
moving disk3 from pole A to pole C
moving disk1 from pole B to pole A
moving disk2 from pole B to pole C
moving disk1 from pole A to pole C
moving disk4 from pole A to pole B
moving disk1 from pole C to pole B
moving disk2 from pole C to pole A
moving disk1 from pole B to pole A
moving disk3 from pole C to pole B
moving disk1 from pole A to pole C
moving disk2 from pole A to pole B
moving disk1 from pole C to pole B
moving disk5 from pole A to pole C
moving disk1 from pole B to pole A
moving disk2 from pole B to pole C
moving disk1 from pole A to pole C
moving disk3 from pole B to pole A
moving disk1 from pole C to pole B
moving disk2 from pole C to pole A
moving disk1 from pole B to pole A
moving disk4 from pole B to pole C
moving disk1 from pole A to pole C
moving disk2 from pole A to pole B
moving disk1 from pole C to pole B
moving disk3 from pole A to pole C
moving disk1 from pole B to pole A
moving disk2 from pole B to pole C
moving disk1 from pole A to pole C
31

Reference

“汉诺塔”算法-之通俗易懂,简单的原理-java编程